Day 5 – 100 days of DSA challenge

Challenge: Container With Most Water

Welcome to Day 5 of our 100 Days DSA Challenge! 🚀 Today, we face a captivating challenge involving elevation maps and the art of trapping rainwater. Let’s dive into the intricacies of computing the maximum amount of water that can be trapped.

The Challenge:

Given an array of non-negative integers representing an elevation map, our task is to compute the maximum amount of water that can be trapped after raining. The width of each bar is 1.

Example:

const heights = [1, 8, 6, 2, 5, 4, 8, 3, 7];
// Output: 49

In this example, the most water (49 units) can be trapped between the 2nd and 9th bars. The width of the container is determined by the indices of the two bars, and the height of the container is determined by the shorter of the two bars.

Challenge Yourself:

Before exploring the solution, challenge yourself to think about how you would approach this problem. Can you optimize the code further?

The Solution:

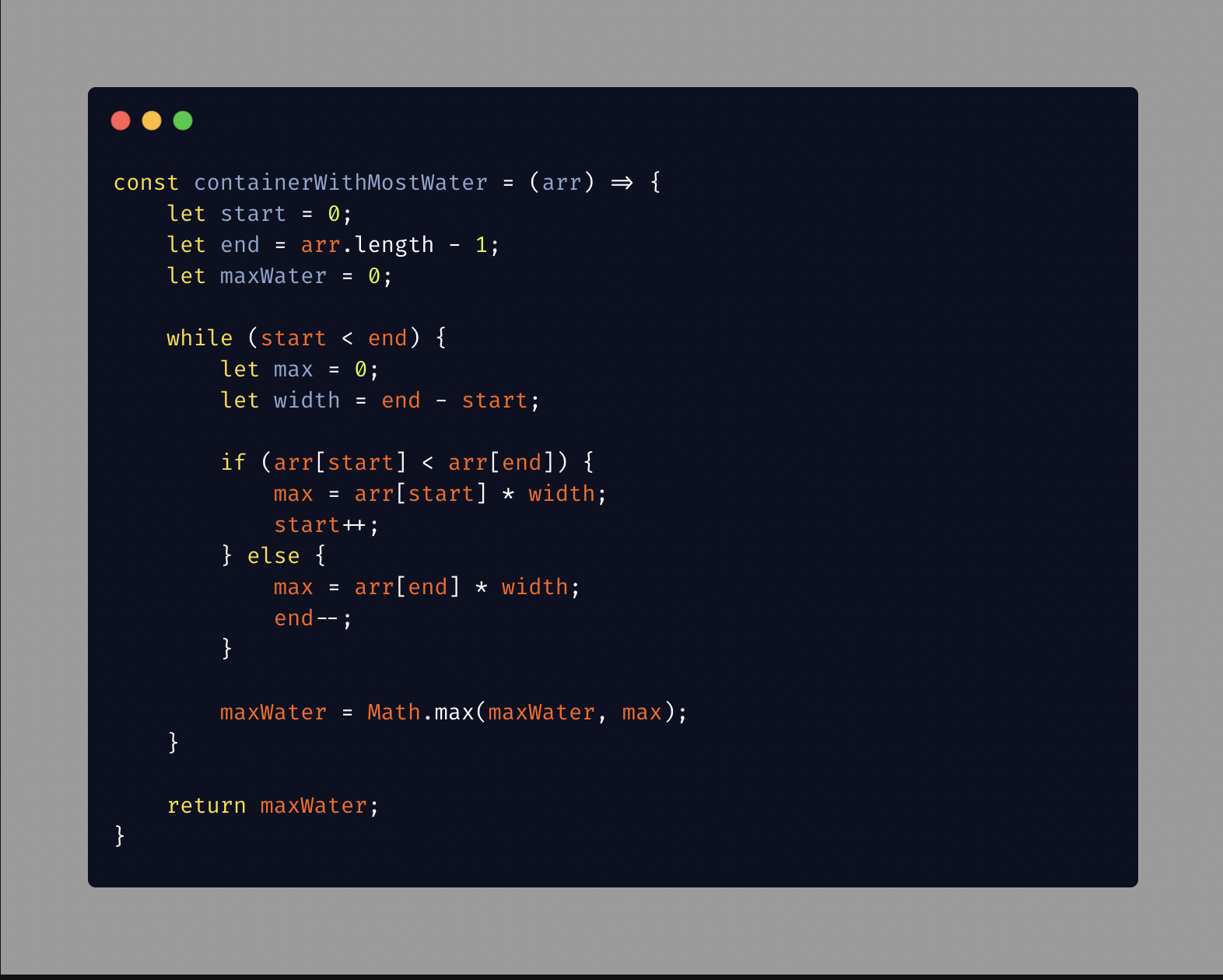
const containerWithMostWater = (arr) => {
    let start = 0;
    let end = arr.length - 1;
    let maxWater = 0;

    while (start < end) {
        let max = 0;
        let width = end - start;

        if (arr[start] < arr[end]) {
            max = arr[start] * width;
            start++;
        } else {
            max = arr[end] * width;
            end--;
        }

        maxWater = Math.max(maxWater, max);
    }

    return maxWater;
}

Solution Logic:

1. Initialize Pointers and Variables:
   • We start with two pointers, start at the beginning of the array and end at the end.
   • maxWater is the variable to keep track of the maximum water that can be trapped.
2. Iterate Towards the Center:
   • We use a while loop to iterate until the start and end pointers meet.
3. Calculate Trapped Water:
   • For each iteration, we calculate the potential trapped water by considering the minimum height between the two bars (determined by arr[start] and arr[end]) multiplied by the width (end - start).
4. Move Pointers Based on Height:
   • We move the pointer associated with the shorter bar, as trapping more water depends on increasing the height of the shorter bar.
5. Update Maximum Trapped Water:
   • We update maxWater with the maximum value obtained in each iteration.
6. Repeat Until Pointers Meet:
   • We repeat these steps until the start and end pointers meet in the center.
7. Return Maximum Trapped Water:
   • The final result is the maximum amount of water that can be trapped.

Conclusion:

Congratulations on completing Day 5 of our DSA Challenge! Trapping water between elevation bars is a captivating problem, and mastering it enhances your algorithmic skills. Stay tuned for tomorrow’s challenge, and keep the coding spirit alive!

Happy coding! 🌟💻

#100DaysDSAChallenge #DataStructures #Algorithms #ProgrammingCommunity #CodeNewbie