Maximizing Water Storage: A Unique Perspective on the Container Problem

Introduction

Imagine a series of vertical lines, each represented by an integer, which extend from the x-axis. Your task is to find the two lines that, together with the x-axis, form a container capable of storing the maximum amount of water. This puzzle challenges your ability to think creatively and find the optimal solution.

In this article, we will delve into this fascinating problem, exploring both a naive approach and a more efficient one. By the end, you’ll not only understand how to find the solution but also appreciate the elegance of the efficient approach.

Problem Statement

You are given an array, height, where height[i] represents the height of the ith vertical line. Your goal is to determine the maximum amount of water that can be held by a container formed by any two vertical lines and the x-axis. However, there’s a rule: you cannot slant the container. It must have straight vertical sides.

Example

To put things into perspective, let’s consider two examples.

Example 1:

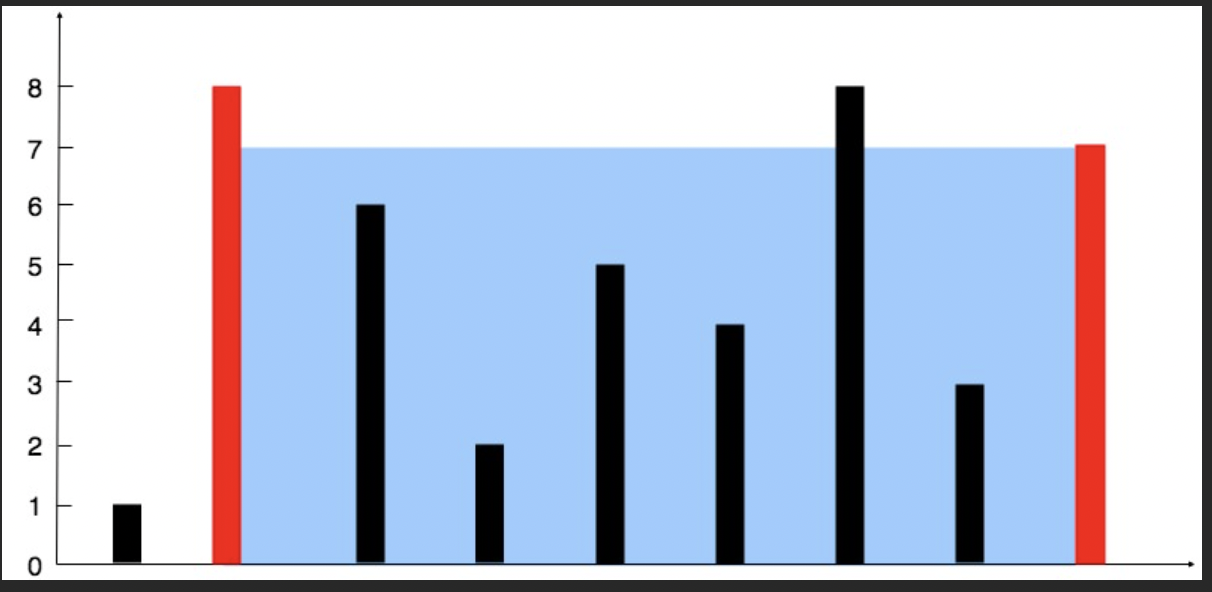
Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49

In this case, the input array represents the heights of the vertical lines. The task is to find the two lines that create a container with the maximum water-holding capacity. In this example, the container formed by lines at positions 2 and 9 (using 0-based indexing) contains the most water, with a capacity of 49 units.

Example 2:

Input: height = [1,1]
Output: 1

In this simpler scenario, there are only two vertical lines, each with a height of 1. The container formed by these two lines and the x-axis can hold 1 unit of water.

The Naive Approach

The naive approach is a straightforward way to solve this problem. It involves calculating the water-holding capacity for all possible pairs of lines and finding the maximum capacity among them. The code for this approach looks like this:

const naiveApproach = (height) => {
    let maxWater = 0;
    for (let i = 0; i <= height.length - 2; i++) {
        for (let j = 1; j <= height.length - 1; j++) {
            let water = Math.min(height[i], height[j]) * (j - i);
            maxWater = Math.max(maxWater, water);
        }
    }
    return maxWater;
}

Algorithm for Naive Approach:

1. Initialize a variable maxWater to 0. This variable will keep track of the maximum water capacity found so far.
2. Use two nested loops to iterate through all possible pairs of lines. The outer loop runs from the first line (0) to the second-to-last line (length – 2), and the inner loop runs from the second line (1) to the last line (length – 1).
3. For each pair of lines (i, j), calculate the water capacity. The capacity is determined by the minimum height between the two lines (Math.min(height[i], height[j])) multiplied by the distance between them (j – i).
4. Compare the calculated water capacity with the current maxWater value. If the calculated capacity is greater, update maxWater with this new value.
5. After both loops complete, return the maxWater, which holds the maximum water capacity found.

The naive approach considers all possible pairs of lines, making it less efficient for larger inputs.

The Efficient Approach

The efficient approach optimizes the solution by using a two-pointer technique. This method avoids calculating the capacity for all possible pairs and instead focuses on finding the best pairs by efficiently adjusting the pointers. Here’s the code for the efficient approach:

const efficientApproach = (height) => {
    let left = 0;
    let right = height.length - 1;
    let maxWater = 0;
    
    while (left < right) {
        const leftValue = height[left];
        const rightValue = height[right];
        const water = leftValue < rightValue ? leftValue * (right - left) : rightValue * (right - left);

        if (water > maxWater) {
            maxWater = water;
        }

        if (leftValue < rightValue) {
            left++;
        } else {
            right--;
        }
    }
    return maxWater;
}

Algorithm for Efficient Approach:

1. Initialize two pointers, left and right, to the beginning and end of the array, respectively.
2. Initialize a variable maxWater to 0. This variable will keep track of the maximum water capacity found so far.
3. Create a while loop that continues as long as the left pointer is less than the right pointer. This loop efficiently adjusts the pointers to find the best pairs.
4. Inside the loop, get the heights of the lines at positions left and right as leftValue and rightValue.
5. Calculate the water capacity for the current pair based on the height of the shorter line leftValue, rightValue and the distance between the pointers (right – left).
6. Compare the calculated water capacity with the current maxWater value. If the calculated capacity is greater, update maxWater with this new value.
7. Now comes the interesting part. If the height of the line at the left pointer is less than the height at the right pointer, increment the left pointer. Otherwise, decrement the right pointer. This step ensures that we always move the pointer pointing to the shorter line, which increases the chances of finding a higher line for the other pointer.
8. Continue this process of adjusting the pointers and updating maxWater until the left pointer is no longer less than the right pointer.
9. After the loop completes, return the maxWater, which holds the maximum water capacity found.

The efficient approach reduces the time complexity significantly and is considered an optimal solution for this problem.

Wrapping Up

The container problem challenges us to think creatively and find the most efficient solution to maximize water storage. While a naive approach does the job, the efficient two-pointer method offers a faster and more elegant solution. Understanding the problem and these two approaches is a great step toward becoming a more versatile problem solver in the world of computer science.

Happy Coding !!